1. Wave Motion and its Applications, Applied Physics -2, (2001), Polytechnic 2nd semester Notes

 

1. तरंग गति और इसके अनुप्रयोग

1.1 तरंग गति

तरंग गति वह प्रक्रिया है, जिसके द्वारा ऊर्जा एक स्थान से दूसरे स्थान तक स्थानांतरित होती है, बिना उस माध्यम के कणों की वास्तविक गति के। यह हवा, पानी और ठोस पदार्थों जैसे विभिन्न माध्यमों में हो सकती है।

• तरंगों के प्रकार:

  1. यांत्रिक तरंगें: इन तरंगों के लिए एक माध्यम की आवश्यकता होती है (जैसे, ध्वनि तरंगें, जल तरंगें, और डोरी पर तरंगें)। ये निर्वात में यात्रा नहीं कर सकतीं।
  2. विद्युतचुंबकीय तरंगें: इन तरंगों को एक माध्यम की आवश्यकता नहीं होती है और ये निर्वात में भी यात्रा कर सकती हैं (जैसे, प्रकाश, रेडियो तरंगें, एक्स-रे)।

  तरंगों को सामान्यतः तरंगदैर्ध्य (λ), आवृत्ति (f), गति (v) और अम्ल (A) द्वारा वर्णित किया जाता है।

---

1.2 अनुप्रस्थ और अनुरेखी तरंगें और उनके उदाहरण

कणों की गति के आधार पर तरंगों का वर्गीकरण:

• अनुप्रस्थ तरंगें:

  • इन तरंगों में, माध्यम के कणों की गति तरंग के प्रसार की दिशा के लम्बवत होती है।
  • उदाहरण: प्रकाश तरंगें, डोरी पर तरंगें, जल तरंगें।
  • मुख्य विशेषताएँ:
    • क्रीस्ट: तरंग का सबसे ऊँचा बिंदु।
    • गर्त: तरंग का सबसे निचला बिंदु।
    • अम्ल: कणों का अधिकतम विस्थापन।
    • तरंगदैर्ध्य: दो लगातार क्रीस्ट या गर्तों के बीच की दूरी।
  

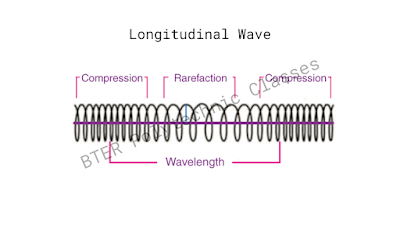
• अनुरेखी तरंगें:

  • इन तरंगों में, कणों की गति तरंग के प्रसार की दिशा के समानांतर होती है।
  • उदाहरण: ध्वनि तरंगें, भूकंपीय P-तरंगें।
  • मुख्य विशेषताएँ:
    • संपीड़न: कणों का घनत्व उच्चतम होता है।
    • विरलन: कणों का घनत्व न्यूनतम होता है।
    • तरंगदैर्ध्य: दो लगातार संपीड़न या विरलन के बीच की दूरी।
  

---

1.3 तरंग गति, आवृत्ति और तरंगदैर्ध्य की परिभाषाएँ और उनका संबंध

• तरंग गति (v):

  • यह वह गति है जिस पर एक तरंग एक माध्यम में यात्रा करती है।
  • सूत्र: $v = \frac{\lambda}{T}$ या $v = f \times \lambda$, जहाँ $T$ समयकाल और $f$ आवृत्ति है।

• आवृत्ति (f):

  • यह वह संख्या है, जो यह बताती है कि एक तरंग प्रति सेकंड कितनी बार दोलन करती है। इसे हर्ट्ज़ (Hz) में मापा जाता है।
  • सूत्र: $f = \frac{1}{T}$, जहाँ $T$ समयकाल है।

• तरंगदैर्ध्य (λ):

  • यह दो लगातार क्रीस्ट या गर्तों के बीच की दूरी है। इसे मीटर (m) में मापा जाता है।

• संबंध:

  • तरंग गति और आवृत्ति और तरंगदैर्ध्य के बीच संबंध निम्नलिखित सूत्र द्वारा व्यक्त किया जाता है: $$v = f \times \lambda$$
    
  • जहाँ:
    • $v$ = तरंग गति (m/s)
    • $f$ = आवृत्ति (Hz)
    • $\lambda$ = तरंगदैर्ध्य (m)

---

1.4 तरंगों के सुपरपोजीशन का सिद्धांत

सुपरपोजीशन का सिद्धांत कहता है कि जब दो या दो से अधिक तरंगें किसी बिंदु पर मिलती हैं, तो परिणामी विस्थापन उस बिंदु पर उन तरंगों के व्यक्तिगत विस्थापन का गणनात्मक योग होता है।

• निर्माणात्मक अभिसंयोजन: जब दो तरंगें एक-दूसरे के अनुरूप होती हैं (क्रीस्ट क्रीस्ट से मिलती है, गर्त गर्त से मिलते हैं), तो उनके विस्थापन जुड़कर एक बड़ी तरंग बनाते हैं।
• विनाशात्मक अभिसंयोजन: जब दो तरंगें आपस में विपरीत दिशा में होती हैं (क्रीस्ट गर्त से मिलते हैं), तो वे एक-दूसरे को समाप्त कर देती हैं, जिससे आयाम घट जाता है।

उदाहरण: यदि दो समान आवृत्ति और आयाम वाली तरंगें मिलती हैं, तो वे एक बड़ी तरंग बना सकती हैं। यदि वे विपरीत दिशा में मिलती हैं, तो वे एक-दूसरे को समाप्त कर देती हैं।

---

1.5 स्थिर तरंगें और संगीतिक ट्यूब

• स्थिर तरंगें:

  • स्थिर तरंगें तब बनती हैं जब दो तरंगें समान आवृत्ति, आयाम और तरंगदैर्ध्य के साथ विपरीत दिशाओं में यात्रा करती हैं और आपस में अभिसंयोजन करती हैं।
  • मुख्य विशेषताएँ:
    • नोड्स: वे बिंदु जहाँ कोई विस्थापन नहीं होता (विनाशात्मक अभिसंयोजन)।
    • एनटिनोड्स: वे बिंदु जहाँ विस्थापन अधिकतम होता है (निर्माणात्मक अभिसंयोजन)।
  • उदाहरण: एक डोरी पर कंपन करती स्थिर तरंग।
  
  
  

  
  

• संगीतिक ट्यूब:

  • संगीतिक ट्यूब एक ऐसा खोखला यंत्र है जिसमें ध्वनि तरंगों के लिए स्थिर तरंगें बनती हैं। जब ध्वनि तरंगों की आवृत्ति ट्यूब की प्राकृतिक आवृत्ति से मेल खाती है, तो संगीतिक प्रभाव उत्पन्न होता है और आयाम बहुत बढ़ जाता है।
  • प्रयोग: संगीतिक ट्यूब का उपयोग हवा में ध्वनि की गति को जानने के लिए किया जाता है।

---

1.6 सरल हार्मोनिक गति (SHM)

1.6.1 परिभाषा

सरल हार्मोनिक गति (SHM) एक प्रकार की गति है जिसमें पुनर्स्थापन बल वस्तु के संतुलन बिंदु से विस्थापन के समानुपाती होता है, और वह बल वस्तु को संतुलन बिंदु की ओर खींचता है।

• मुख्य विशेषताएँ:

  • यह गति आवर्तक होती है (समय के साथ दोहराई जाती है)।
  • विस्थापन एक साइनसाइडल पैटर्न का पालन करता है।
  • पुनर्स्थापन बल को हुक के नियम द्वारा व्यक्त किया जाता है: $F=-k\mathrm{x,\; जहाँ:}$
    • $F$ पुनर्स्थापन बल है।
    • $k$ वसंत स्थिरांक (या बल स्थिरांक) है।
    • $x$ संतुलन बिंदु से विस्थापन है।

• गति का समीकरण: SHM का समीकरण इस प्रकार होता है:

  $$x(t) = A \cos(\omega t + \phi)$$
  

  जहाँ:

  • $A$ = गति की अधिकतम विस्थापन (अम्ल)।
  • $\omega$ = कोणीय आवृत्ति।
  • $\phi$ = चरण स्थिरांक।
  • $t$ = समय।

---

1.6.2 सरल हार्मोनिक प्रगति तरंग और ऊर्जा स्थानांतरण

• सरल हार्मोनिक प्रगति तरंग:

  • SHM में प्रगति करने वाली तरंग एक प्रकार की तरंग होती है जो एक माध्यम के माध्यम से यात्रा करती है और ऊर्जा को एक स्थान से दूसरे स्थान तक स्थानांतरित करती है, बिना उस माध्यम के कणों को बड़े पैमाने पर स्थानांतरित किए।

• SHM में ऊर्जा:

  • कुल ऊर्जा (E) SHM में वह ऊर्जा होती है जो गति और स्थिति के बीच स्थानांतरित होती है।
  • कुल ऊर्जा का सूत्र: $$E = \frac{1}{2} m \omega^2 A^2$$जहाँ:
    • $m$ = द्रव्यमान।
    • $\omega$ = कोणीय आवृत्ति।
    • $A$ = अम्ल।

---

प्रश्नों का अभ्यास

लंबे उत्तर वाले प्रश्न:

1. तरंगों के सुपरपोजीशन सिद्धांत को समझाइए और इसके वास्तविक जीवन में अनुप्रयोगों का वर्णन कीजिए।

   • उत्तर: सुपरपोजीशन का सिद्धांत कहता है कि जब दो या दो से अधिक तरंगें किसी बिंदु पर मिलती हैं, तो परिणामी विस्थापन उस बिंदु पर उन तरंगों के व्यक्तिगत विस्थापन का योग होता है। निर्माणात्मक अभिसंयोजन में, तरंगें जोड़कर एक बड़ी तरंग बनाती हैं और विनाशात्मक अभिसंयोजन में, वे एक-दूसरे को समाप्त करती हैं, जिससे आयाम घट जाता है। इस सिद्धांत का उपयोग ध्वनि तरंगों (जैसे, शोर-रद्द करने वाले हेडफोन), प्रकाश तरंगों, और जल तरंगों में किया जाता है।

2. सरल हार्मोनिक गति (SHM) का वर्णन कीजिए और इसका गति का समीकरण व्युत्पन्न कीजिए।

   • उत्तर: SHM वह गति है जिसमें पुनर्स्थापन बल वस्तु के विस्थापन के समानुपाती होता है। इसका समीकरण इस प्रकार होता है: $$F = -kx$$ न्यूटन का द्वितीयक नियम: $$F = ma = m \frac{d^2x}{dt^2}$$ बलों को मिलाकर: $$m \frac{d^2x}{dt^2} = -kx$$ इसे पुनः व्यवस्थित करके: $$\frac{d^2x}{dt^2} + \frac{k}{m} x = 0$$यह SHM का समीकरण है, जहाँ $\frac{k}{m} = \omega^2$ है, और $\omega$ कोणीय आवृत्ति है।

सांख्यिकी समस्याएँ:

1. एक तरंग की आवृत्ति 50 Hz है और तरंगदैर्ध्य 2 मीटर है। तरंग गति ज्ञात करें।

   • समाधान: दिए गए:
     • $f = 50$
       
     • $\lambda =\mathrm{2\; मीटर\; सूत्र }$$v = f \times \lambda$ का उपयोग करते हुए:
     $$v = 50 \times 2 = 100 \text{ m/s}$$अतः, तरंग गति 100 मीटर/सेकंड है।

2. एक सरल पेंडुलम 10 सेंटीमीटर की अम्ल के साथ और 2 Hz की आवृत्ति से दोलन करता है। पेंडुलम की अधिकतम गति ज्ञात करें।

   • समाधान: दिए गए:
     • $A = 10$ सेंटीमीटर = 0.1 मीटर
     • $f = 2$ Hz
     • कोणीय आवृत्ति $\omega = 2\pi f = 2\pi \times 2 = 4\pi$  रैड/सेकंड अधिकतम गति (v_max) का सूत्र:
     $$v_{\text{max}} = A\omega = 0.1 \times 4\pi = 1.2566 \text{ m/s}$$ अतः, अधिकतम गति $1.2566$ मीटर/सेकंड है।

---

महत्वपूर्ण MCQ प्रश्न

1. तरंग गति की SI इकाई क्या है?

   • A) मीटर
   • B) मीटर/सेकंड
   • C) हर्ट्ज़
   • D) सेकंड
   • उत्तर: B) मीटर/सेकंड

2. कौनसी तरंगें अनुरेखी तरंगें हैं?

   • A) प्रकाश तरंगें
   • B) ध्वनि तरंगें
   • C) जल तरंगें
   • D) रेडियो तरंगें
   • उत्तर: B) ध्वनि तरंगें

3. सरल हार्मोनिक गति में पुनर्स्थापन बल के लिए समीकरण क्या है?

   • A) $F = ma$
     
   • B) $F = -kx$
     
   • C) $F = mv^2$
     
   • D) $F = mg$
     
   • उत्तर: B) $F = -kx$